Interests
Multivariate Splines My main interest lies in the theory and application of multivariate splines which I have studied for over twenty years.Multivariate splines are smooth piecewise polynomial functions defined on triangulation(2D) or tetrahedral partition(3D) or simplicial partition (mD). These
functions are computer compatiable and can be used for approximating unknown or known functions. I mainly study the approximation properties of multivariate splines, construction of locally supported spline functions, approximation properties of data fitting using multivariate splines, computation with multivariate splines. A typical paper that represents my work can be found in On the Approximation Power of Bivariate Splines, where Schumaker and I established the approximation order of bivariate splines in L_p norm for
1<= p <=\infty, where degree of splines is bigger or equal to 3r+2 and r is the
smoothness of spline functions. In this paper , Chui and I found the representation of polynomials in terms of integer translates of multivariate box splines.
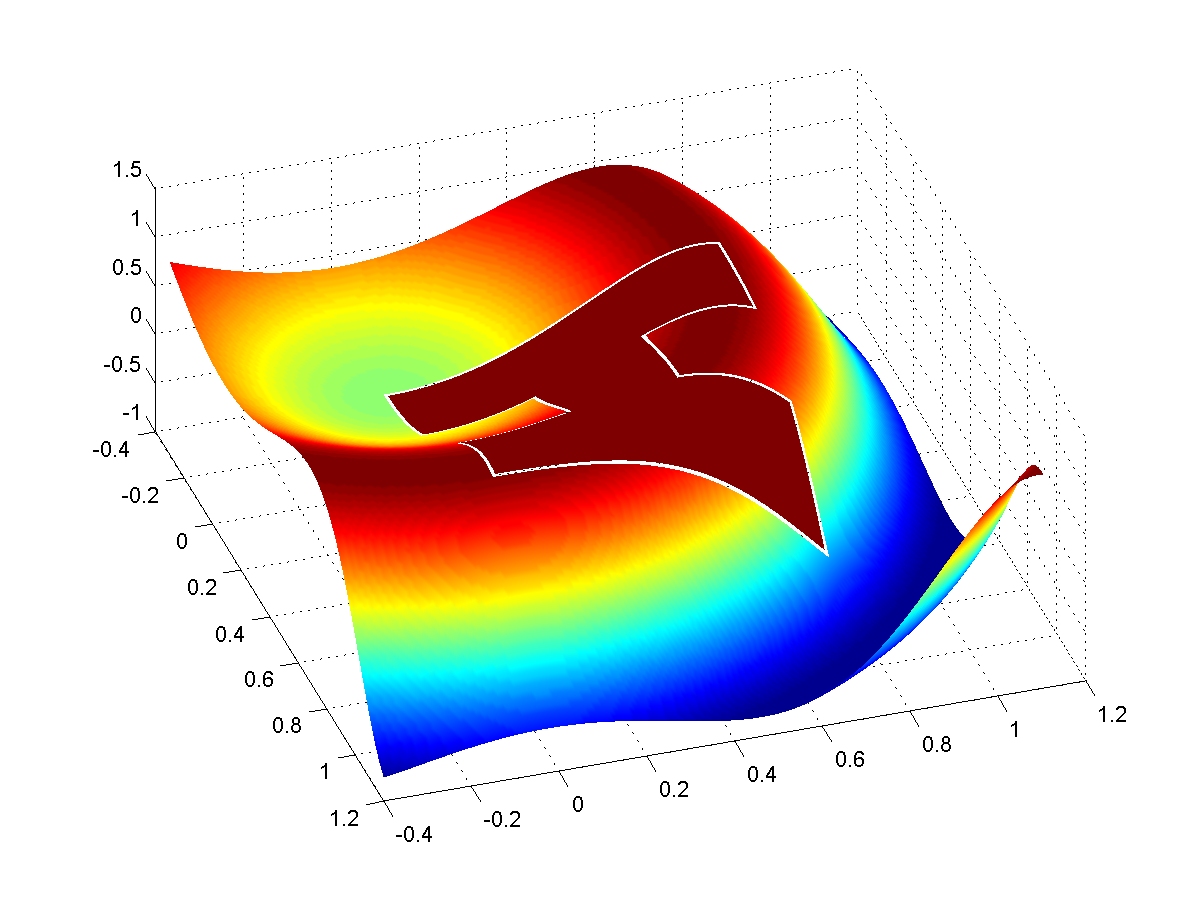
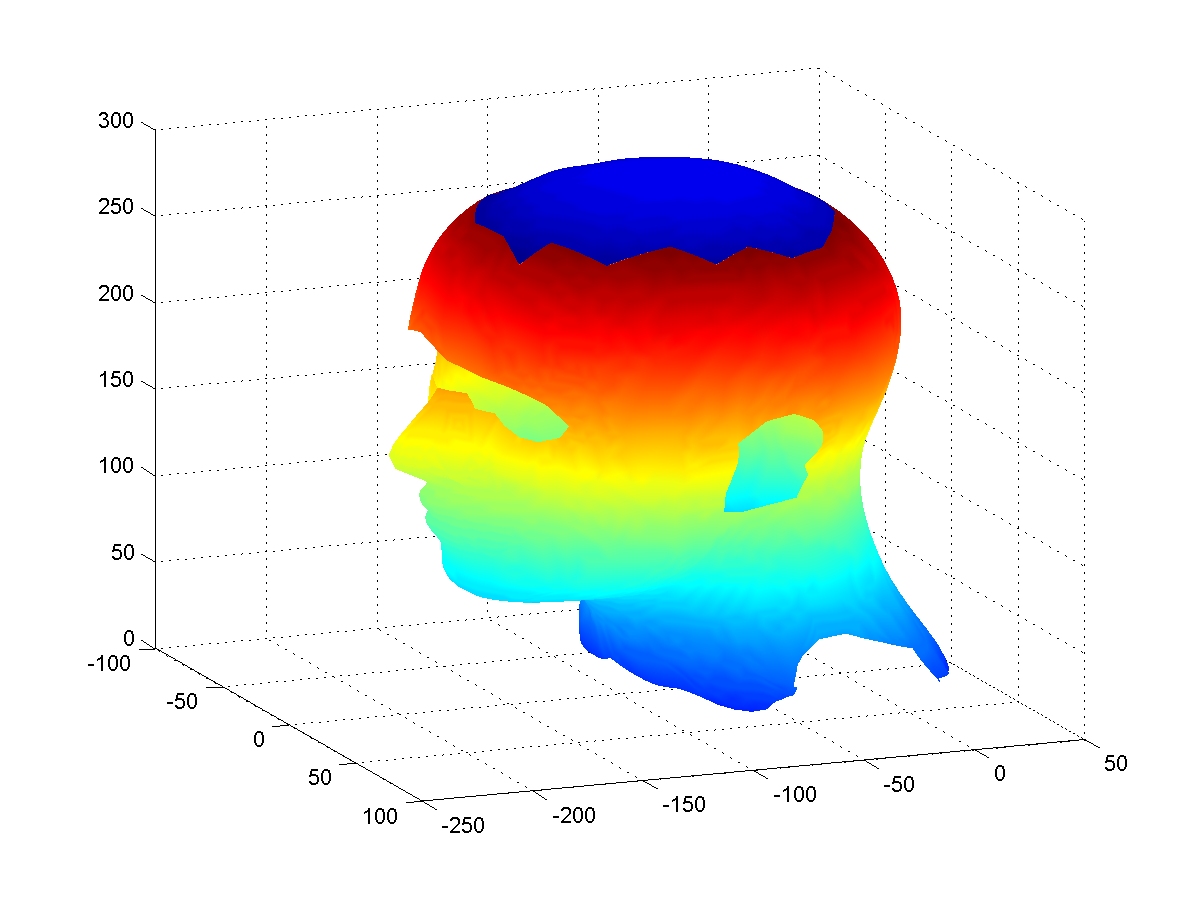
Multivariate splines have various applications in data fitting and hole filling in Computer Aided Geometric Design, Fluid Flow Simulation, in Geodetic Applications,in Image Enhancements and in data prediction.
With Awanou, Baramedize and Wenston, I have implemented bivariate splines, trivariate splines, and spherical splines
in MATLAB. The usefulness of these multivariate splines can be seen in a Ph.D., at the aerospace engineering department of Delft University of Technology, Netherlands 's usage for a global system of identification based on a NASA wind tunnel dataset and other data sets. See Visser's Dissertation.
Wavelets I have also studied the analysis of wavelets and their application for image processing for more than ten years. 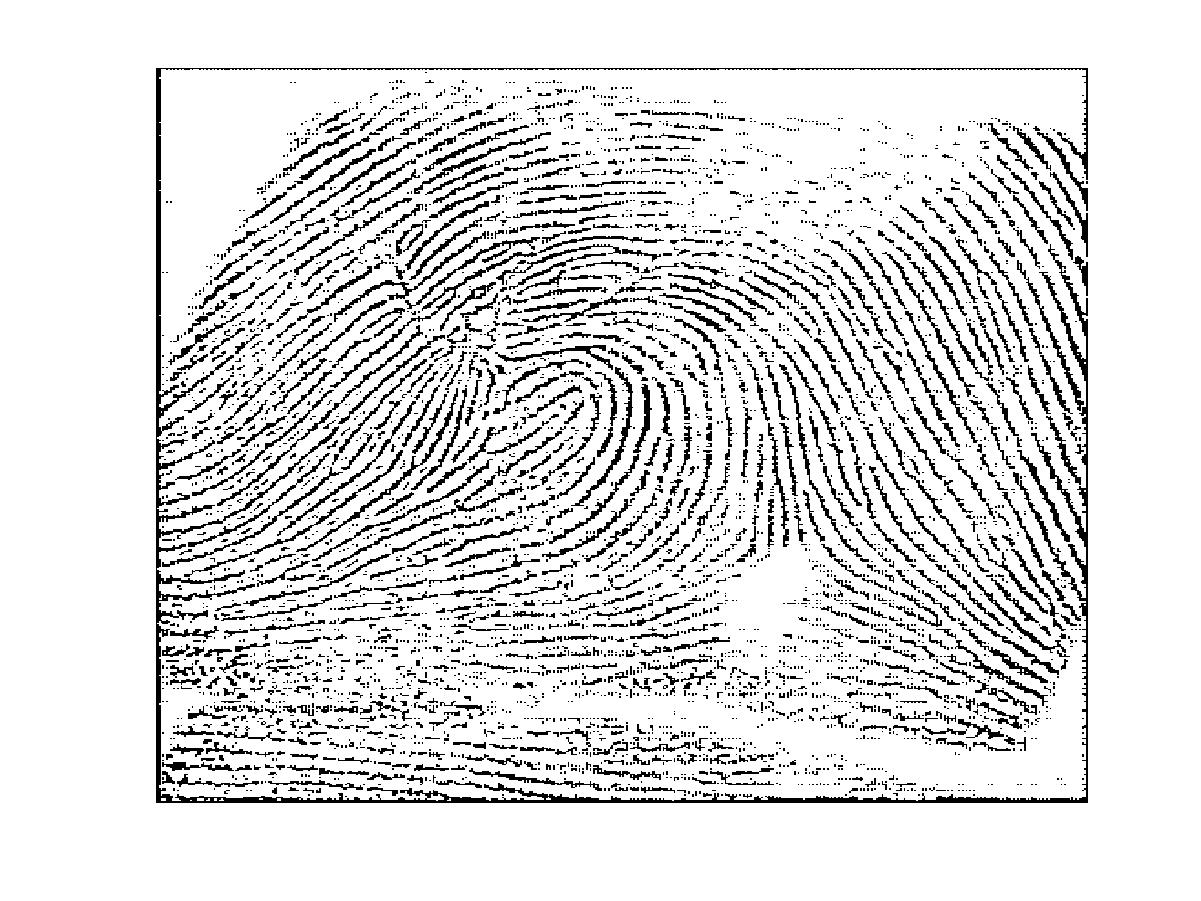 My interest is to construct various compactly supported orthonormal wavelets, orthonormal multi-wavelets, tight wavelet frames based on multivariate box spline functions, multivariate biorthogonal wavelets with arbitrary regularity , multivariate pre-wavelets and pre-Riesz basis , bivariate box spline wavelets in Sobolev spaces . These wavelets
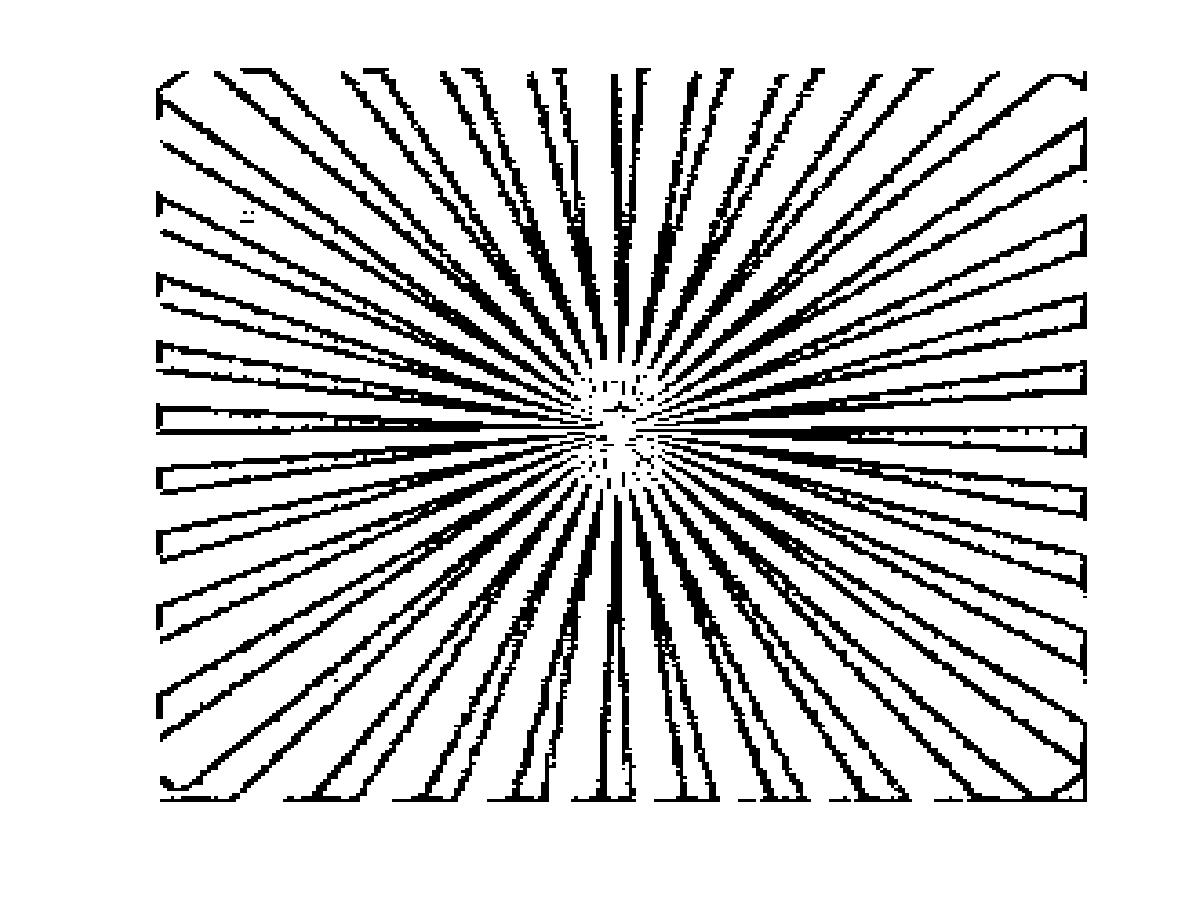
are based on multivariate box splines. The regularity of box splines are known and so are the regularity of these biorthogonal wavelets, prewavelets and pre-Riesz basis, and tight wavelet frames. In addition, I have implemented these tight wavelet frames in bivariate box splines in MATLAB and used them for image processing such as edge detection, image denoising, image compression.
My interest is to construct various compactly supported orthonormal wavelets, orthonormal multi-wavelets, tight wavelet frames based on multivariate box spline functions, multivariate biorthogonal wavelets with arbitrary regularity , multivariate pre-wavelets and pre-Riesz basis , bivariate box spline wavelets in Sobolev spaces . These wavelets
are based on multivariate box splines. The regularity of box splines are known and so are the regularity of these biorthogonal wavelets, prewavelets and pre-Riesz basis, and tight wavelet frames. In addition, I have implemented these tight wavelet frames in bivariate box splines in MATLAB and used them for image processing such as edge detection, image denoising, image compression.
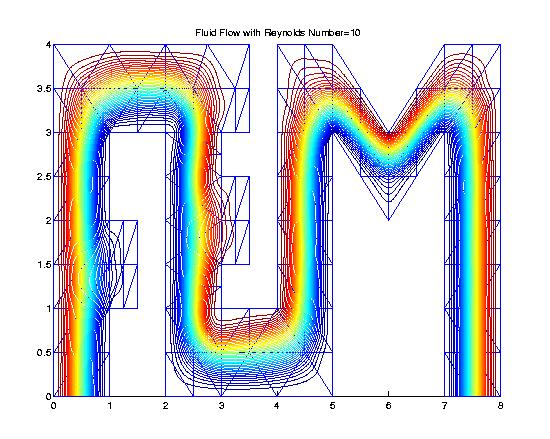
PDE  I am also interested in numerical solutions of PDE by using multivariate splines. In numerical solution of 2D Navier-Stokes equations, I used the stream function formulation instead of common approaches of velocity-pressure formulation or vorticity pressure formulation. The significance of the stream function formulation is that one do not need boundary condition for pressure functions and one solves one stream function instead of two velocity components and one pressure function.
Numerical simulation can be found at here. Recently, I use bivariate splines to solve the nonlinear PDE associated with image denoising, image inprinting, and image enhancements. Numerical results can be found at this page. One significant result I obtained is to establish the convergence of the discrete solution from finite difference method for the nonlinear PDE associated with the ROF model to the theoretical solution of the PDE. See our paper. In addition, I have also established the convergence of the discrete solution from the preojected gradient method to the minimizer of the ROF model. Check my paper for detail.
I am also interested in numerical solutions of PDE by using multivariate splines. In numerical solution of 2D Navier-Stokes equations, I used the stream function formulation instead of common approaches of velocity-pressure formulation or vorticity pressure formulation. The significance of the stream function formulation is that one do not need boundary condition for pressure functions and one solves one stream function instead of two velocity components and one pressure function.
Numerical simulation can be found at here. Recently, I use bivariate splines to solve the nonlinear PDE associated with image denoising, image inprinting, and image enhancements. Numerical results can be found at this page. One significant result I obtained is to establish the convergence of the discrete solution from finite difference method for the nonlinear PDE associated with the ROF model to the theoretical solution of the PDE. See our paper. In addition, I have also established the convergence of the discrete solution from the preojected gradient method to the minimizer of the ROF model. Check my paper for detail.
Currently I am interested in sparest solutions of undetermined linear systems and their applications in compressed sensing and other areas. In my joint paper with Simon Foucart, we show how to use quasi norm lq, 0 < q ≤ 1 to find the sparsest solution. Louis Yang and I solved open problems raised by S. Foucart and his collaborator in 2009. Jingyue Wang and I worked on iterative solution of unconstrained lq minimization. Check my paper at this link. More results are coming....
I maintain a list of research problems to do for the rest of my life. See some of them at here.
Finally, my Erdos number is 2 and my h-index is 10 as Aug. 10, 2011. That is, at least 10 papers each of which has been cited 10 times based on AMS MathSciNet. See google scholars for more citation information.