Fluid Flow

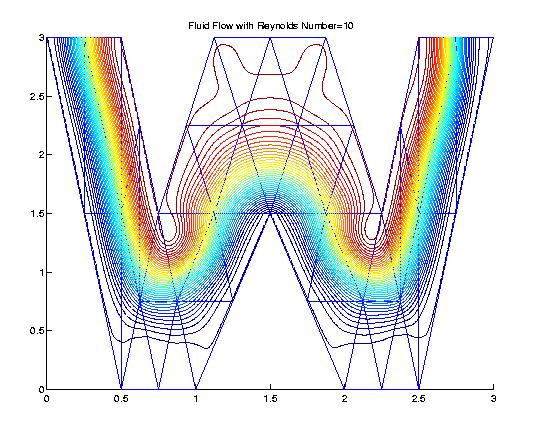
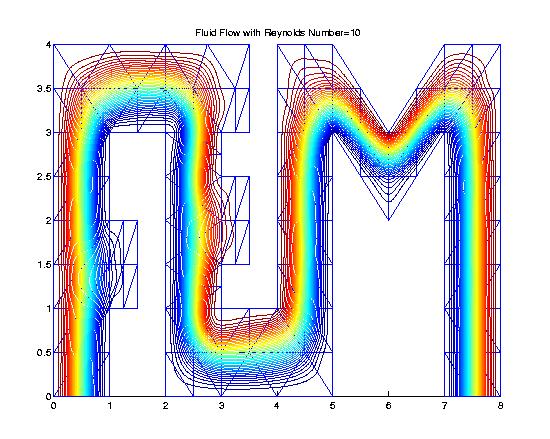
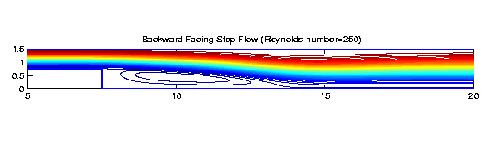
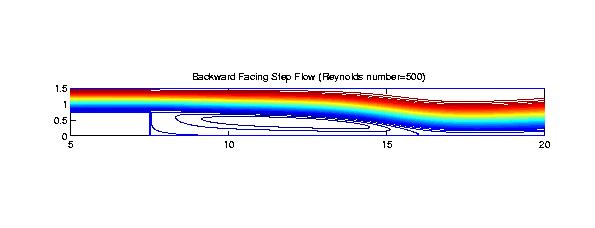
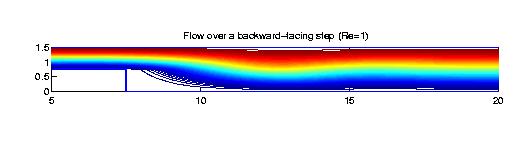
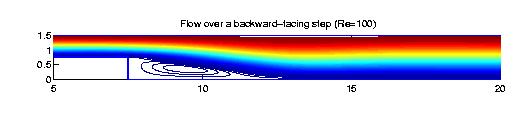
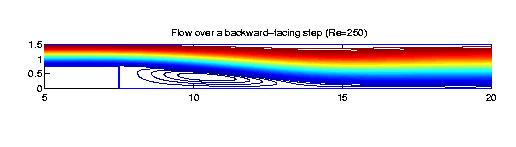
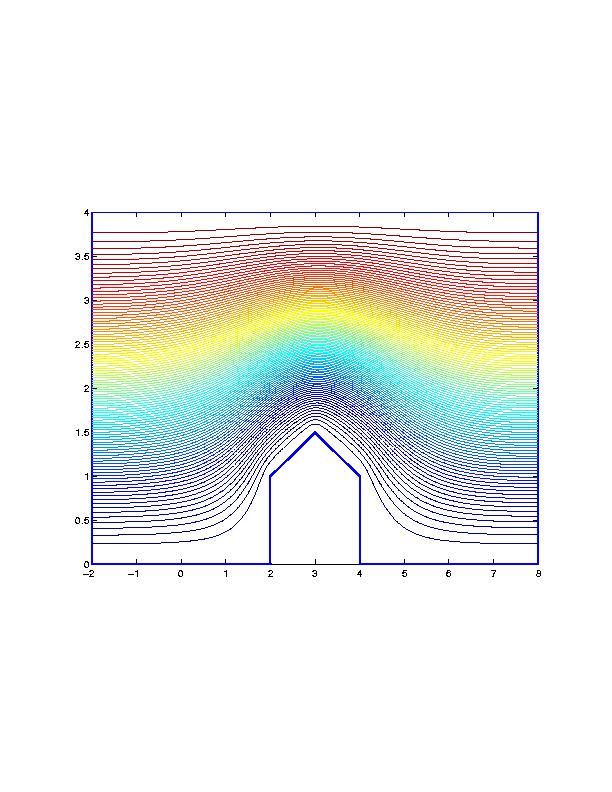
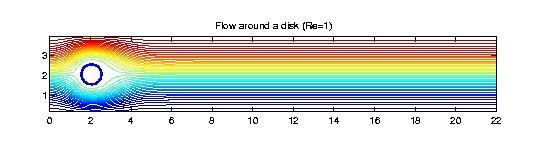
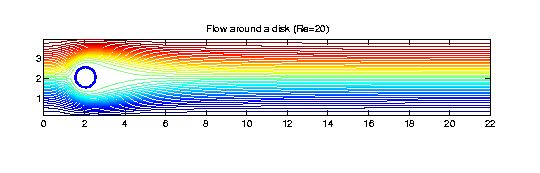
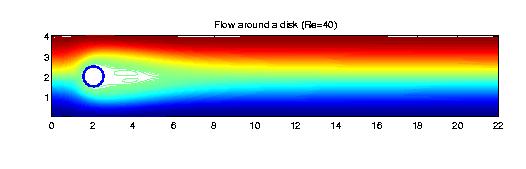
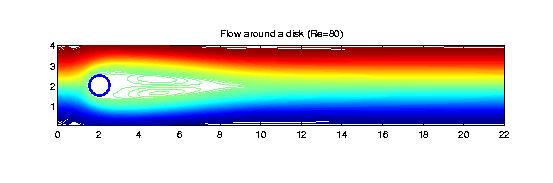
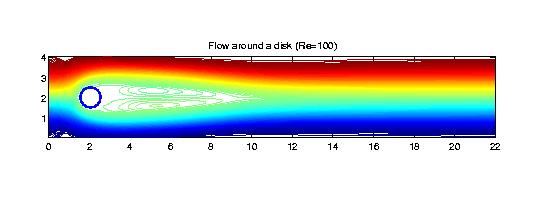
Fluid Flow Simulations We use bivariate splines to solve 2D steady-state Navier-Stokes equations. The main features of our methods are (1) the stream function formulation that is used so that the divergent free condition is satisfied exactly; (2) splines of higher degree and more smoothness are used so that the vorticity is a continuous function; (3) the solutions with higher Reynolds numbers can be computed easily (see examples below); (4) Navier-Stokes equations over arbitrary polygonal domains can be solved; (5) our methods are very efficient and effective. All the following numerical experiments were performed on a Sun workstation with 172 Mhz and a PC laptop with 400 Mhz. I did not use any supercomputers nor any parallel processes.

Cavity Driven Flow The following are standard cavity driven flows with various Reynolds numbers: 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000, 11000, 12000, 13000, 14000, 15000, 16000, 17000, 18000, 19000, 20000.

The vorticity of the cavity driven flows can be found here. 1, 100, 1000.

The following flow image is of flow stream lines over a "W" shaped channel.

THe following are flow streamlines over an FEM-shape Channel

The backward facing step flows with various Reynold numbers are given below.

The following is the water flow around an inclined plate.

The Following is the wind flow around a house.

The following is the water flow pass a rectangular box.

The following are flows are circular obstacle with various Reynold numbers.

I also used bivariate splines to simulate the air flows around two cars. See more fluid flow simulations in a paper by Lai and Wenston in 2004.