Splines

Multivariate splines are piecewise polynomial functions of certain smoothness. To be more precise, let us consider the spline functions in the Euclidean spaces &;¹, ℜ², ℜ³, and sphere S².

Univariate Splines let [a, b] be an interval and P = {a = x₀, x₁, … x_n = b} be a partition of [a, b]. A spline function s of degree d and smoothness r is a r time continuously differentiable function over[a, b] and is a polynomial of degree d when restricted to [x_i, x_i+1] for each i = 0, … , n-1. One of the applications of univariate splines is to design font curves. The outline of a letter, say A is a spline curve so that you can fill in any color, rotate the curves around, and etc. For example, you can enlarge the size of the letters to any size while keeping a smooth shape (by evaluating more points on the curve). See some examples of letters: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, and etc. See an aerobatic alphabet.

Bivariate Splines Let T be a triangulation in ℜ². That is, T consists of nonoverlapping triangles and T has such a property that the intersection of any two triangles is either empty, or is their common vertex, or is their common edge. A spline function s of degree d and smoothness r over triangulation T is an r time continuously differentiable function over the polygonal domain U_{{t\in T}t} and is a polynomial of total degree d when restricted to triangle t for each t of T. One application of bivariate splines is to fit given scattered data. Here is an example of scattered data locations and a triangulation.

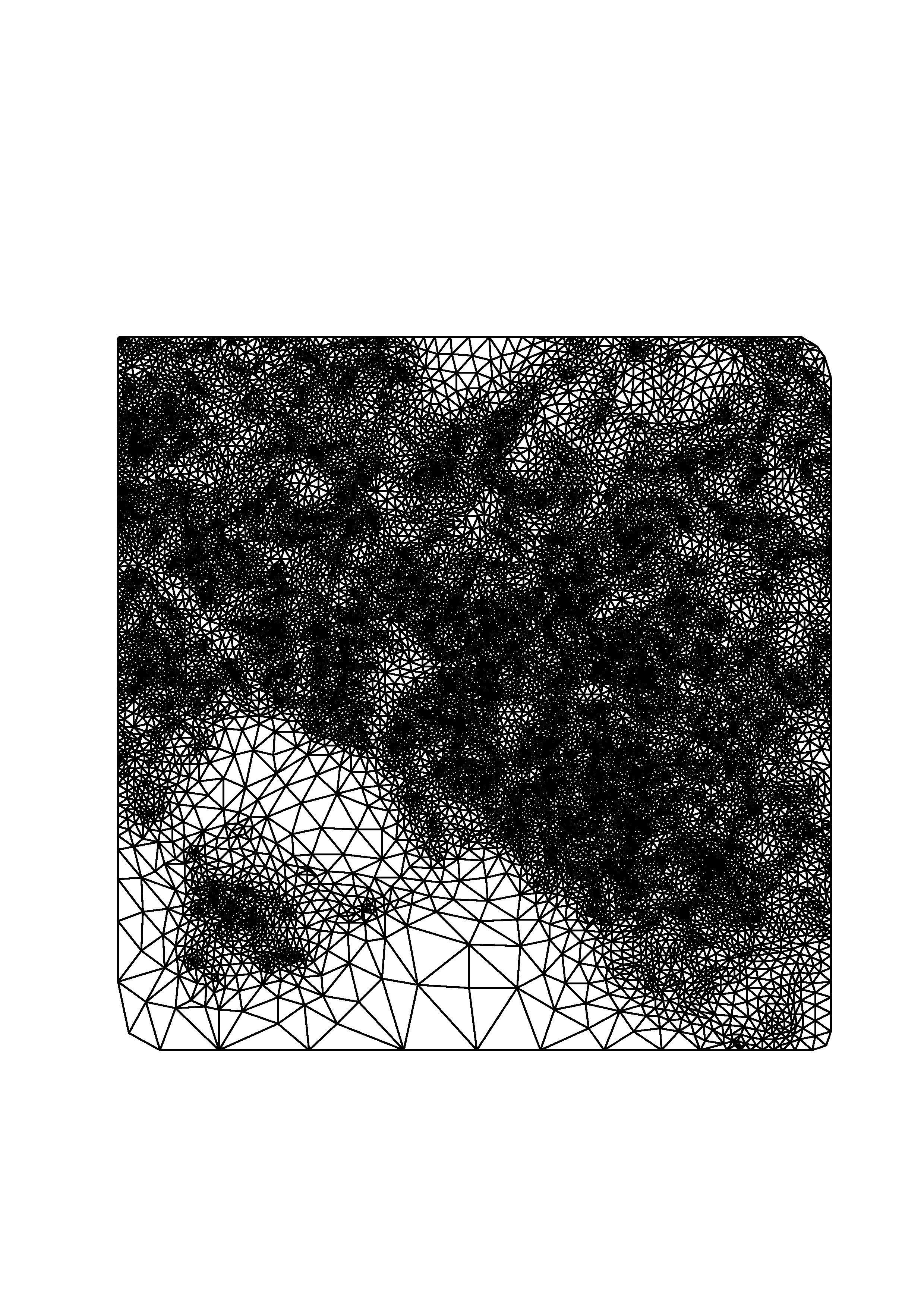
These functions are very flexible and can be efficiently manipulated. There are many applications in areas such as surface design, scattered data fitting, and numerical solutions to partial differential equations such as fluid flow simulation To see how to find a spline interpolation to the given data, see a C¹ cubic spline interpolation using the minimal energy method based on domain decomposition technique. An enlargement of a section is also shown to see that it is indeed a smooth surface. My former Ph.D. student Jane Hong specializes on bivariate splines for image enhancements.

To see more examples, check this out.

Trivariate Splines Let T be a union of tetrahedra in ℜ³. That is T consists of nonoverlapping tetrahedra and T has such a property that the intersection of any two triangles is either empty, a common vertex, a common edge, or a common face. A spline function s of degree d and smoothness r is an r time continuously differentiable function over the polygonal domain U and is a polynomial of total degree d when restricted to tetrahedron t for each t of T. A typical application is to numerically solve partial differential equations. My former Ph.D. student, G. Awanou, specializes on 3D splines for numerical PDE. In particular, we use 3D splines to solve 3D Navier-Stokes equations together. Certainly, it can be used to solve scattered data interpolation.

Spherical Splines Let T be a union of spherical triangulation on a sphere. A spline function s of degree d and smoothness r over T can be defined as well. A typical application is to interpolate data over the earth. My former Ph.D. student V. Baramidze specializes on spherical splines and scattered data fitting.