Multivariate splines are piecewise polynomial functions of certain smoothness. To be more precise, let us consider the spline functions in Euclidean spaces R^1, R^2, R^3, and sphere S^2.
Univariate Splines:
Let [a,b] be an interval and P={a = x_0, x_1, x_2 , ... , x_n =b} be a partition of [a, b]. A spline function s of degree d and smoothness r is a r time continuously differentiable function over [a, b] and is a polynomial of degree d when restricted to [x_i, x_{i+1}] for each i=0, ..., n-1. One of applications of univariate splines is to design font curves. The outline of a letter, say A is a spline curve so that you can fill in any color, rotate the curves around, and etc. For example, you can enlarge the size of the letters to any size while keeping smooth shape (by evaluating more points on the curves). See some examples of letters: A , B , C , D , E , F , G , H , I , J , K , L , M , N, O , P , Q , R , S , and etc. See an aerobatic alphabet.
Bivariate Splines:
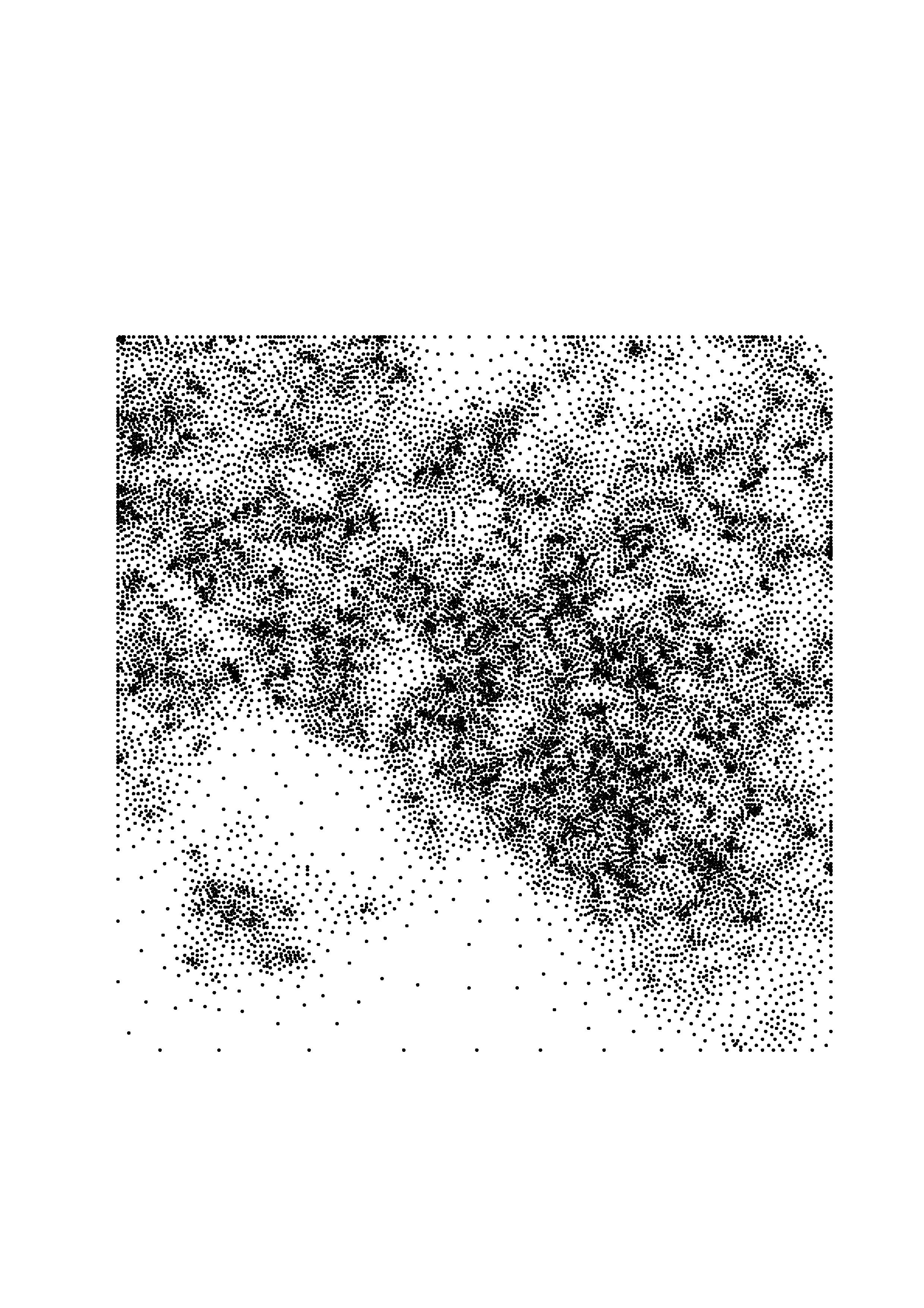
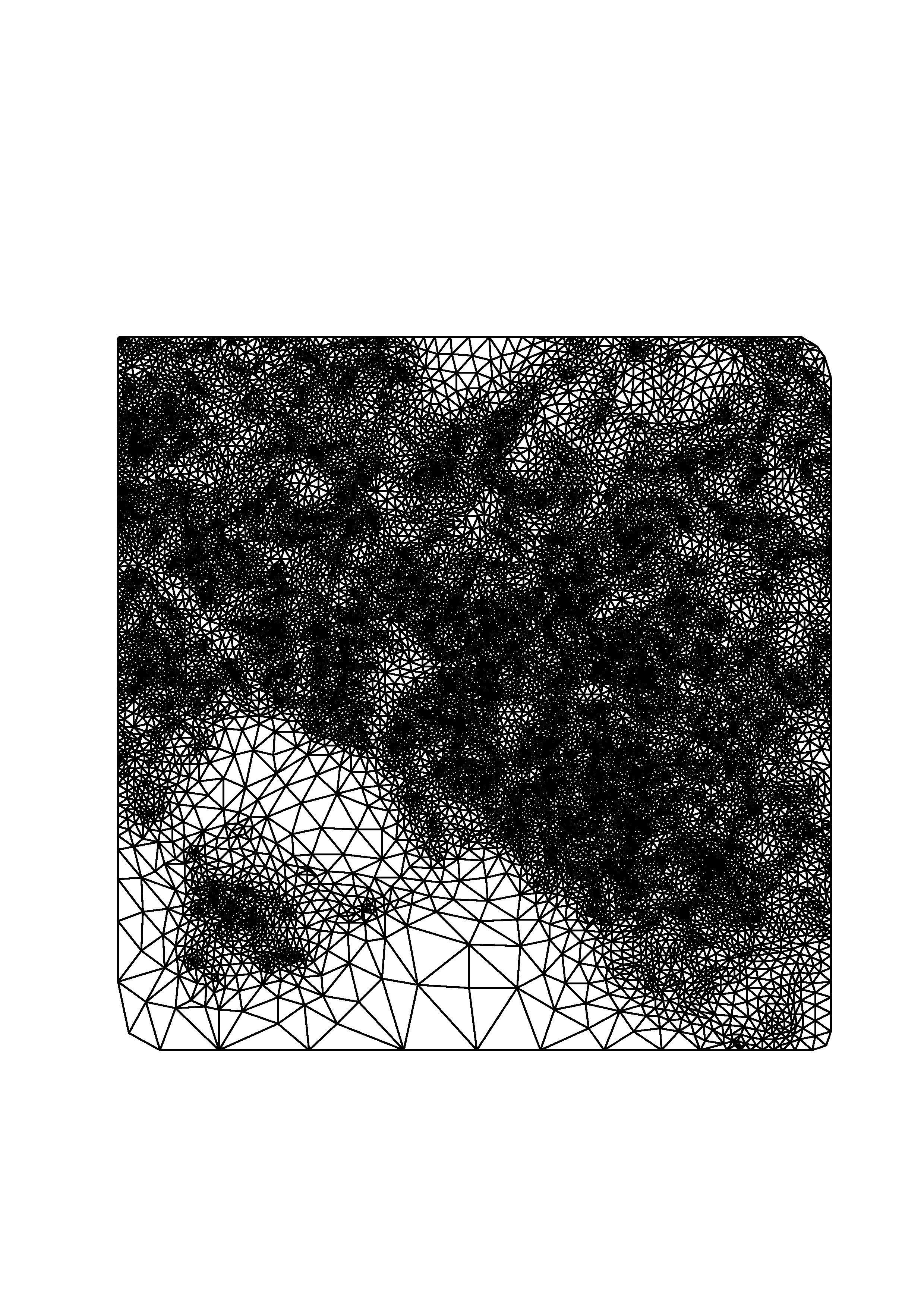
Let T be a triangulation in R^2. That is, T consists of nonoverlapping triangles and T has such a property that the intersection of any two triangles is either empty, or their common vertex, or their common edge. A spline function s of degree d and smoothness r over triangulation T is a r time continuously differentiable function over the polygonal domain U_{t\in T}t and is a polynomial of total degree d when restricted to triangle t for each t of T. One application of bivariate splines is to fit given scattered data. Here is an example of scattered data locations and a triangulation.


These functions are very flexible and can be efficiently manupilated. They find many applications in surface design , scattered data fitting , and numerical solution to partial differential equations such as fluid flow simulation . To see some examples, choose the keywords in the above. To see how to find a spline interpolation to the given data, see a C^1 cubic spline interpolation using the minimal energy method based on domain decomposition technique. An enlargement of a section is also shown to see that it is indeed smooth surface.
To compare with our solution, a TIN (terrain interpolation network) is included. An enlargement of the same section is shown as well. You can see that the surface is continuous piecewise linear.
To see more examples, check out here
Trivariate Splines:
Let T be a union of tetrahedra in R^3. That is, T consists of nonoverlapping tetrahedra and T has such a property that the intersection of any two triangles is either empty, or their common vertex, or their common edge, or their common face. A spline function s of degree d and smoothness r over T is a r time continuously differentiable function over the polygonal domain U_{t\in T}t and is a polynomial of total degree d when restricted to tetrahedron t for each t of T. A typical application is to numerically solve partial differential equations. My Ph.D. student G. Awanou is specialized on 3D splines for numerical PDE. In particular, we use 3D splines to solve 3D Navier-Stokes equations. Certainly, it can be used to solve scattered data interpolation.
Spherical Splines:
Let T be a union of spherical triangulation on sphere. A spline function s of degree d and smoothness r over T can be dedined as well. A typical application is to interpolate data over the earth. My Ph.D. student V. Baramidze is specialied on spherical splines and scattered data fitting.
There is a vast literature on multivariate splines available online. Check Multivariate Spline Bibliography.
The following is my publications on multivariate splines.
Ming-Jun Lai's Papers on Multivariate Splines[36] M. J. Lai and L. L. Schumaker, Trivariate Cr polynomial macro-elements, accepted for publication in Constructive Approxi., 2006. [35] V. Baramidze, M. J. Lai, and C. K. Shum, Spherical Splines for Data Interpolation and Fitting, accepted for publication in SIAM J. Scientific Computing, 2005. [34] G. Awanou and M. J. Lai, On the convergence rate of the augumented Lagrangian algorithm for the nonsymmetric saddle point problem, J. Applied Numerical Mathematics, (54) 2005, 122--134. [33] G. Awanou and M. J. Lai, Trivariate Spline Approximations of 3D Navier-Stokes Equations , accepted for publication in Mathematics of Computation, 2004. [32] M.J.Lai and P. Wenston, Bivariate Splines for Fluid Flows, Computers and Fluids 33(2004), pp. 1047--1073. [31] M. J. Lai, Chun Liu, and Paul Wenston, On two nonlinear biharmonic evolution equations, accepted for publication in Applicable Analysis, 2003. [30] M. J. Lai, Chun Liu, and Paul Wenston, Numerical simulation of two nonlinear biharmonic equations, accepted for publication in Applicable Analysis, 2003. [29] M. J. Lai, Chun Liu, and Paul Wenston, Bivariate spline method for numerical solution of time evolution Navier-Stokes equations over polygons in stream function formulation, Numerical Methods for P. D. E., 2003 pp. 776--827. [28] $C^1$ quintic spline interpolation over tetrahedral partitions, (with G. Awanou) in Approximation Theory X: Wavelets, Splines and Applications, edited by C. K. Chui, L. L. Schumaker, J. Stoeckler, Vanderbilt Univ. Press, 2002, pp. 1--16. [27] A new kind of trivariate $C^1$ finite element (with A. LeMehaute), 2002. to appear in Advances in Computational Math., 2003. [26] L1 Spline Methods for Scattered Data Interpolation and Approximation (with Paul Wenston), to appear in Advances in Computational Mathematics, 2002. [25] Trivariate $C^1$ cubic splines for numerical solution of biharmonic equations (with Paul Wenston), in: {\sl Trends in Approximation Theory}, K. Kopotun, T. Lyche, and M. Neamtu (eds.), Vanderbilt University Press, Nashville, 2001, pp. 224--234. [24] Quadrilateral macro-elements, (with Larry Schumaker), accepted for publication in SIAM J. Math. Anal., 2001. [23] Macro-elements and stable local bases for splines on Powell-Sabin triangulations (with Larry Schumaker), to appear in Math. Comp., 2001. [22] Macro-elements and stable local bases for splines on Clough-Tocher triangulations (with Larry Schumaker), Numer. Math., 88(2001), pp. 105-119. [21] On the approximation power of splines on triangulated quadrangulations (with Larry Schumaker), SIAM J. Num. Anal., 36 (1999), pp. 143--159. [20] Scattered Data Interpolation by $C^2$ Quintic Splines Using Energy Minimization (with Kathleen W. Farmer), in Approximation Theory IX: Computational Aspects Charles K. Chui and Larry L. Schumaker (eds.) Vanderbilt University Press (Nashville), 1998, pp. 47--54. [19] Approximation power of bivariate splines (with Larry Schumaker), Advances in Comput. Math., 9(1998), pp. 251--279 [18] Scattered Data interpolation using piecewise polynomials of degree six(with Larry Schumaker), SIAM Numer. Anal., 34(1997), pp. 905--921. [17] On C^2 Quintic Spline Functions Over Triangulations of Powell-Sabin's Type, Journal of Computational and Applied Mathematics, 73(1996), pp. 135--155. [16] Scattered data interpolation and approximation by C^1 piecewise cubic polynomials, Comput. Aided Geom. Design, 13(1996), 81--88. [15] Bivariate Spline Spaces on FVS-triangulations, Approximation Theory VIII, C. K. Chui and L. L. Schumaker (eds.), 309--316, World Scientific Publishing, 1995. [14] Approximation order from bivariate C^1 cubics on a four--directional mesh is full, Comput. Aided Geometric Design, 11(1994), pp. 215--223. [13] A Serendipity family of locally supported splines in S^2_8(\triangle), J. Approx. Theory and Appl. 10(1993), pp.. 43--53. [12] A characteristic theorem of multivariate splines in blossom form, Comput. Aided Geometric Design, 8(1992), pp. 513--521. [11] Algorithms for generating B-nets and graphically displaying box spline surfaces, (with C.K. Chui), Compt. Aided Geometric Design, 8(1992), pp. 479--493. [10] Fortran subroutines for B-nets of box splines on three and four directional meshes, Numerical Algorithm, 2(1992), pp. 33--38. [9] On bivariate super vertex splines, (with C.K. Chui), Constr. Approx., 6(1990), pp. 399-419. [8] Multivariate vertex splines and finite elements, (with C.K. Chui), J. Approx. Theory, 60(1990), pp. 245-343. [7] A remark on integer translates of a box spline, J. Approx. Applic., 5(1989), pp. 97--104. [6] Construction of real-time spline quasi-interpolation scheme, (with G. Chen and C.K. Chui), J. Approx. Applic., 4(1988), pp. 61--75. [5] Multivariate analog of Marsden's identity and a quasi-interpolation scheme, (with C.K. Chui), Constr. Approx., 3(1987), pp. 111-122. [4] On multivariate vertex splines and applications, (with C.K. Chui), Topics in Multivariate Approximation, Chui, C.K., L.L. Schumaker, and F. Utreras eds. Academic Press, 1987, pp. 19-36. [3] Computation of box splines and B-splines on triangulations of nonuniform rectangular partitions, (with C.K. Chui), J.Approx. Applic., 3-4(1987), pp. 37-62. [2] On bivariate vertex splines, (with C.K. Chui), Multivariate Approximation theory III, W.Schempp and K.Zeller, eds., Birkh\"auser, 1985, pp. 84-115. [1] On estimations for the exact bounds of the coefficients of approximation by cubic spline interpolation, Math. Numer. Sinica, 6(1984), pp. 105-108. |