On this page, I use three examples to explain how to use spherical splines (cf. Chapters 13--14 in my book coauthored with Larry Schumaker) to do data interpolation/fitting problems over the spherical spline setting.
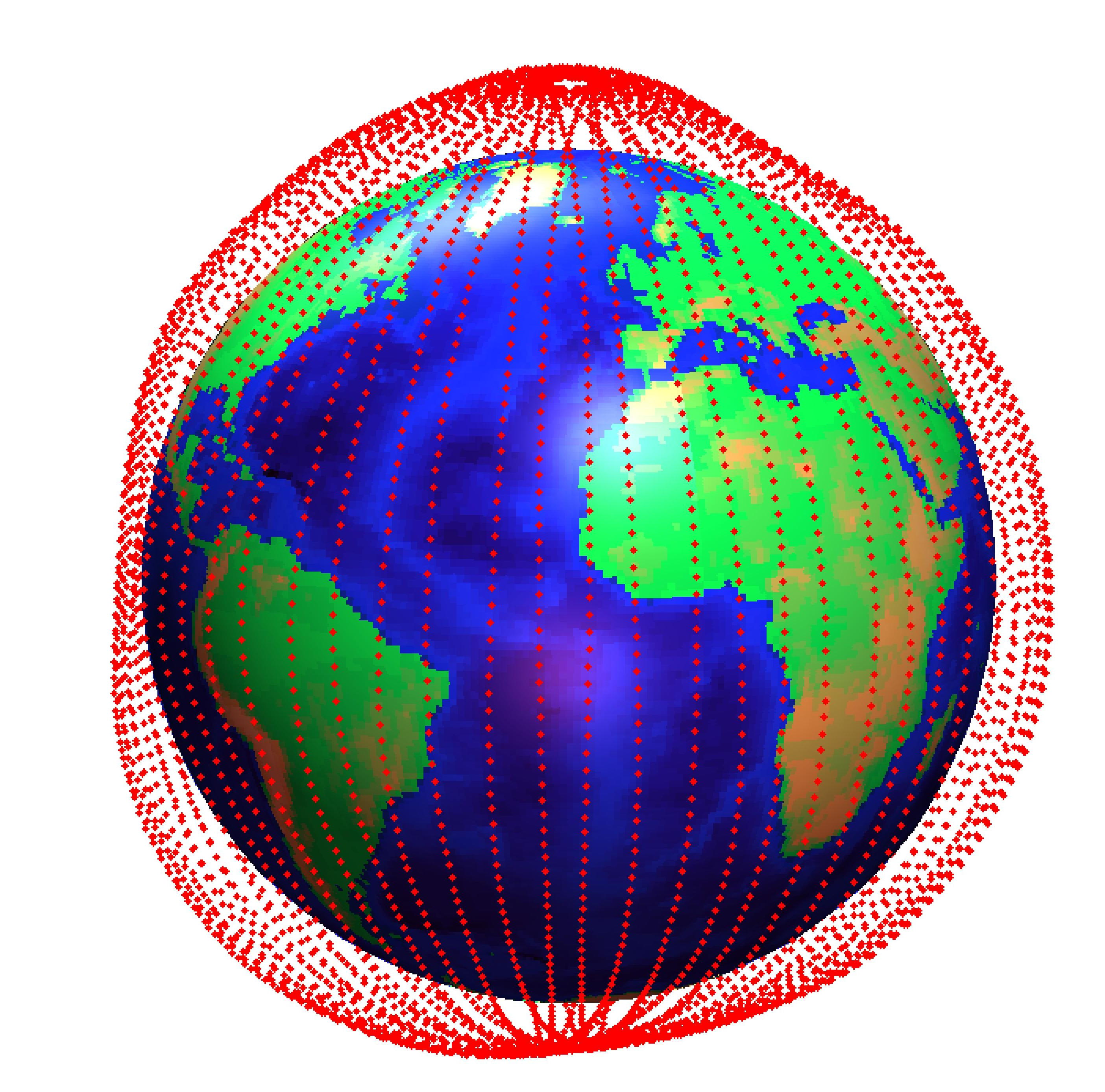
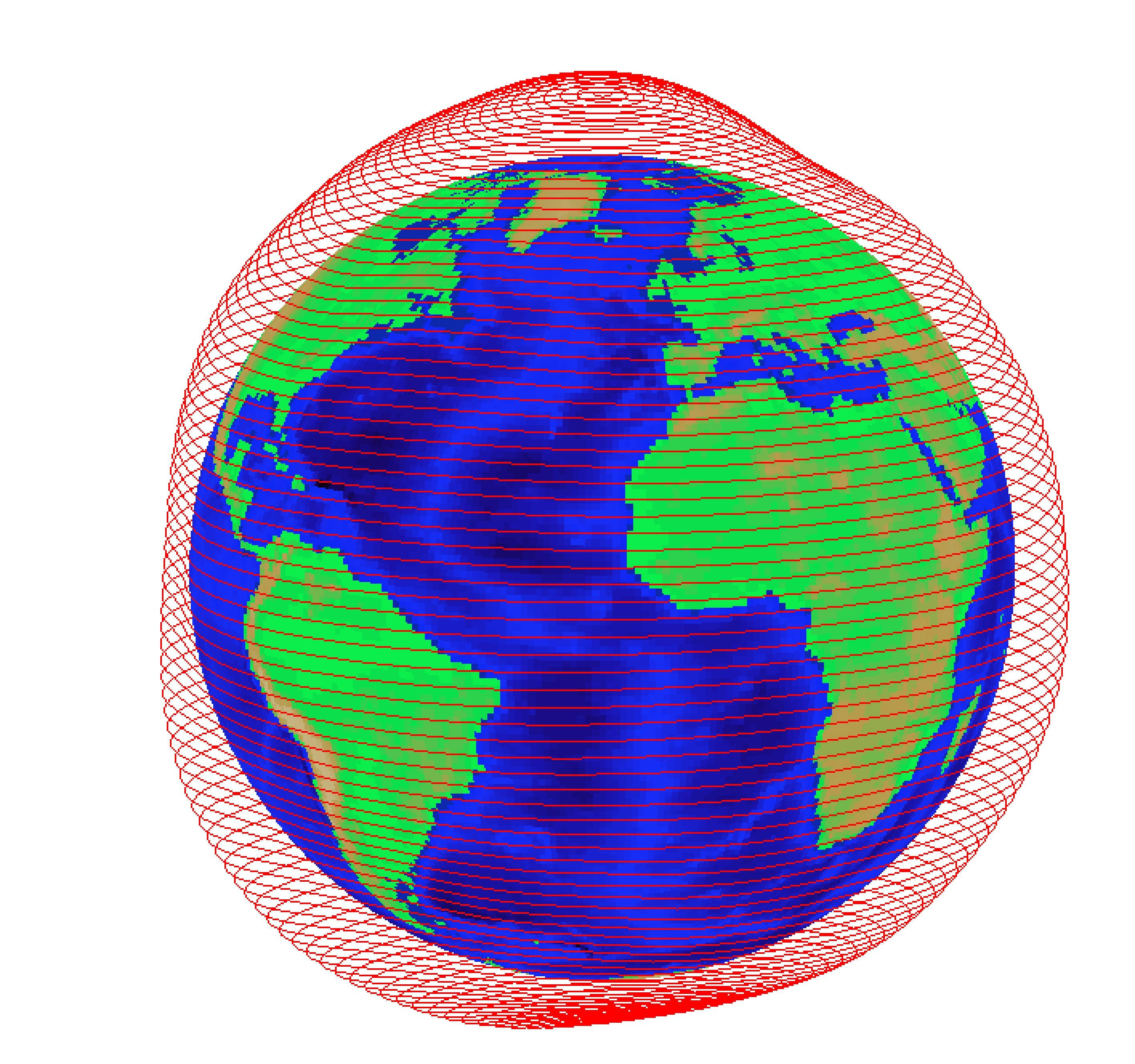
Example 1. We got a set of data which are measurements of the geopotential from a satellite over a period of two day. They are simulated data for a German satellite CHAMP which was launched in 2000 and was circulated at an orbit at 450 km high above the surface of the Earth. The left is the corresponding measurement locations and the right is a triangulation of the Earth surface.


Example 2. A set of data is given describing a car body. We use a spherical spline to find a smooth interpolatory surface of the car body. Instead of building car hood, roof, doors and etc., separately and matching their boundaries of different pieces carefully to achieve a smooth match, we can construct the whole car body by using one surface and then cut the hood, roof, doors out of the whole surface. See the following figures. Let us have a data set with refined triangulation. We show them with and without a moonroof.
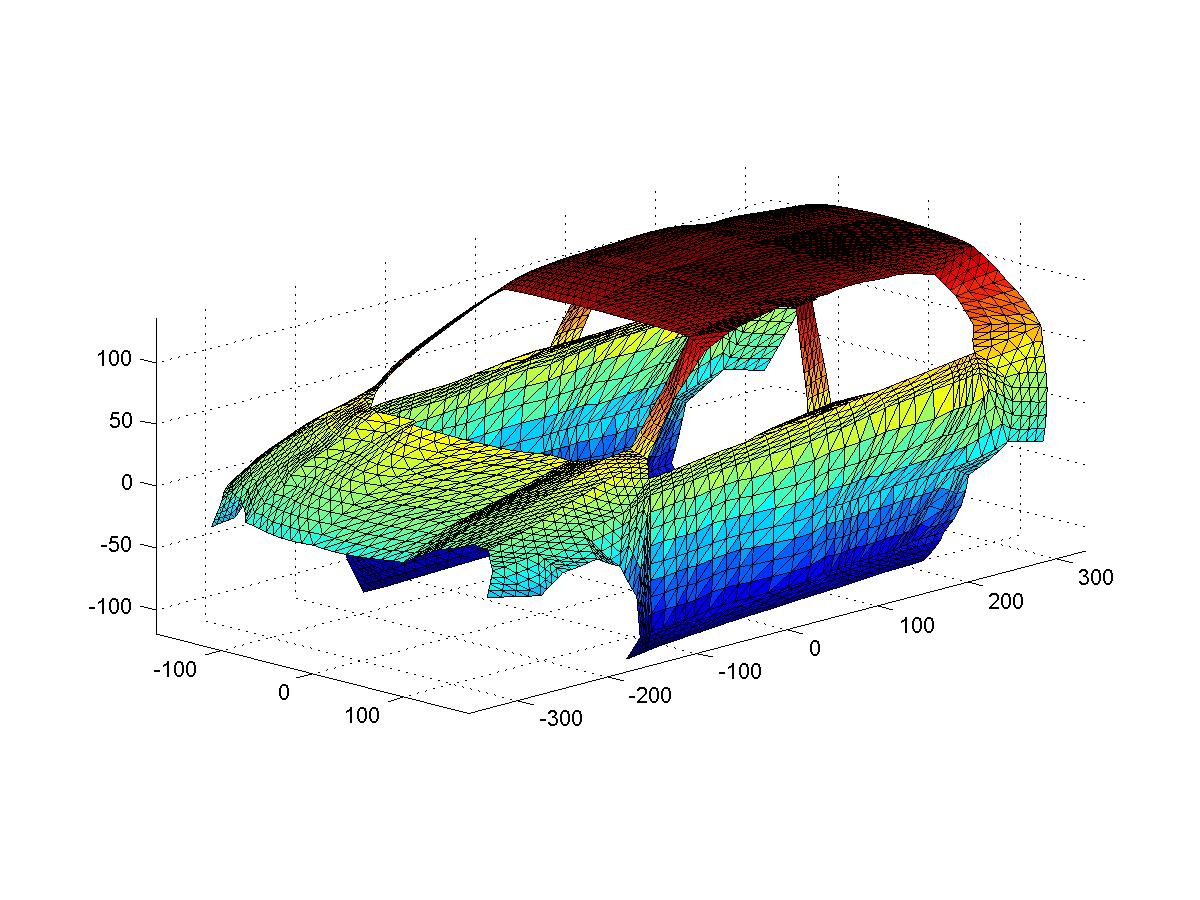
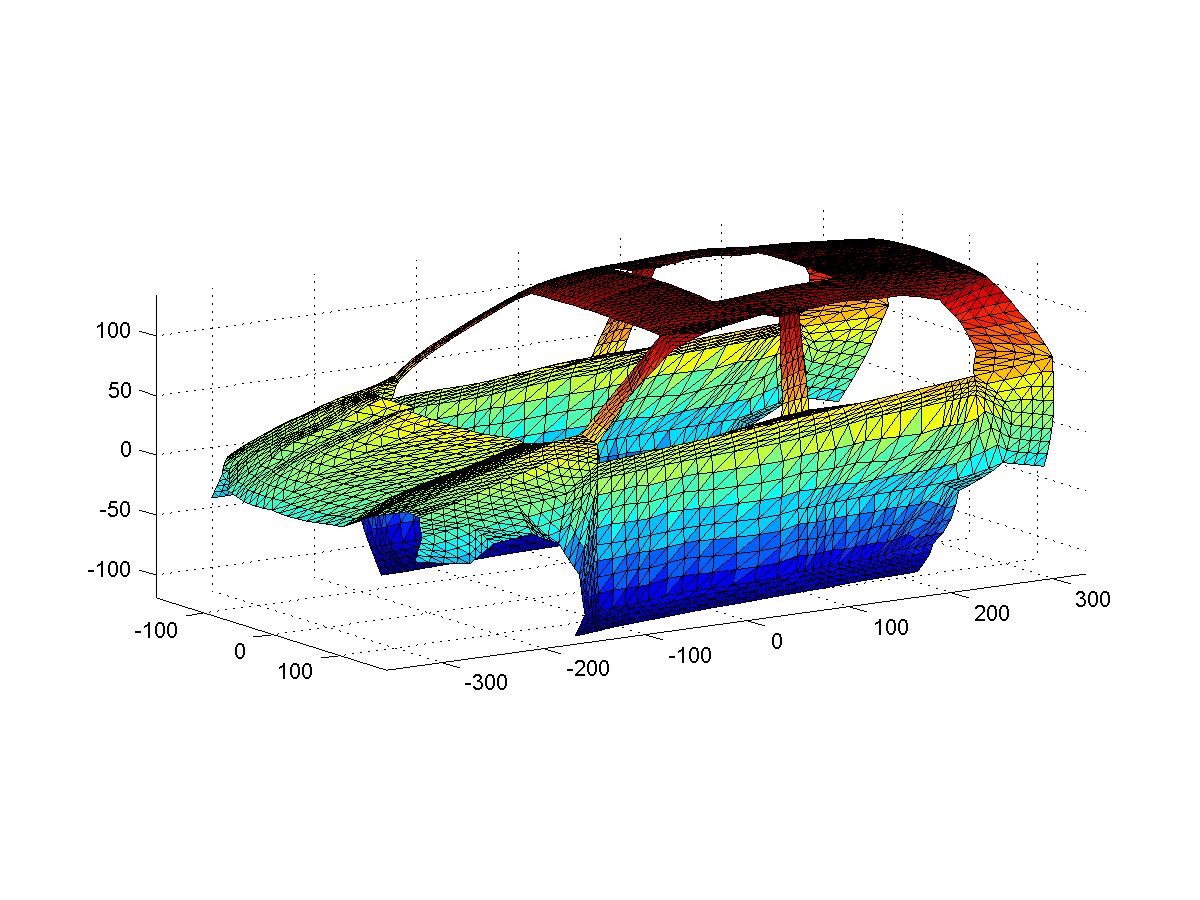
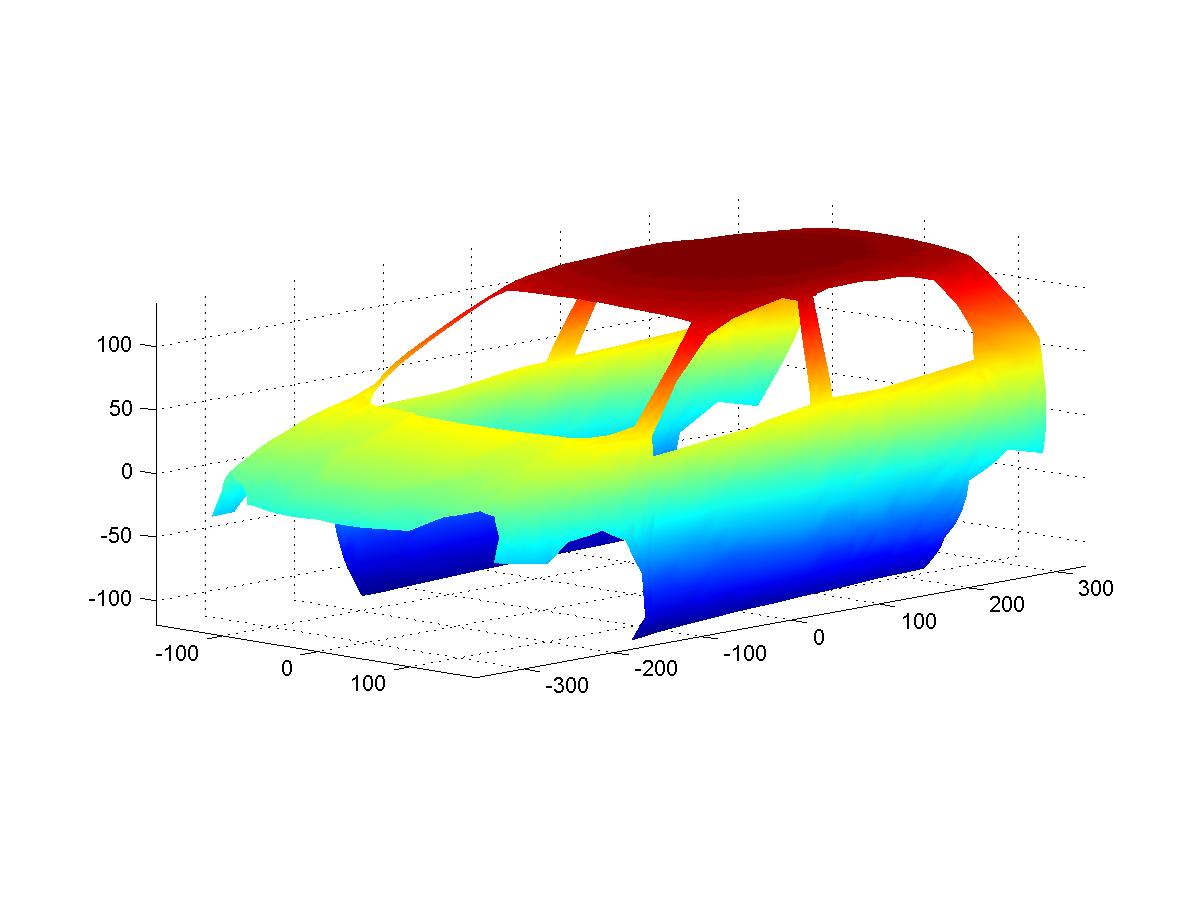
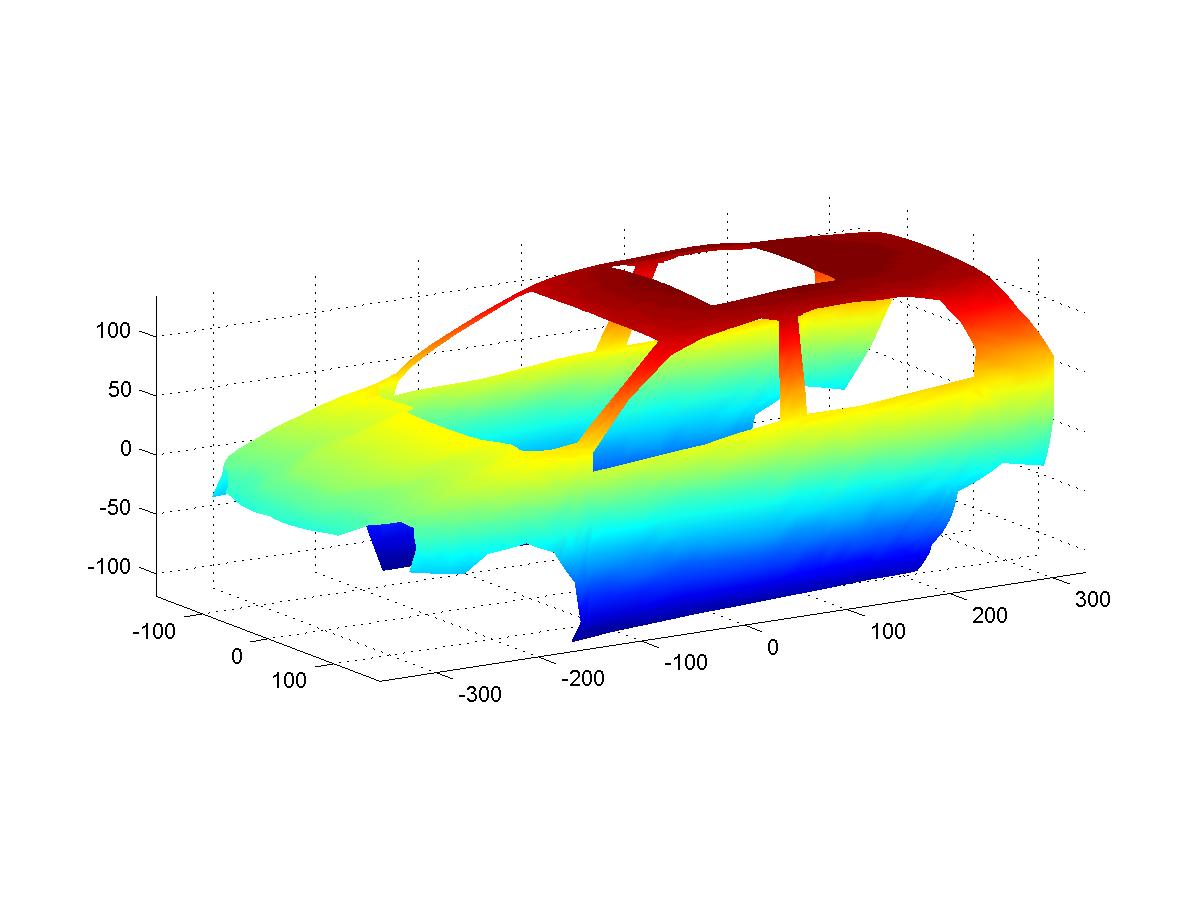
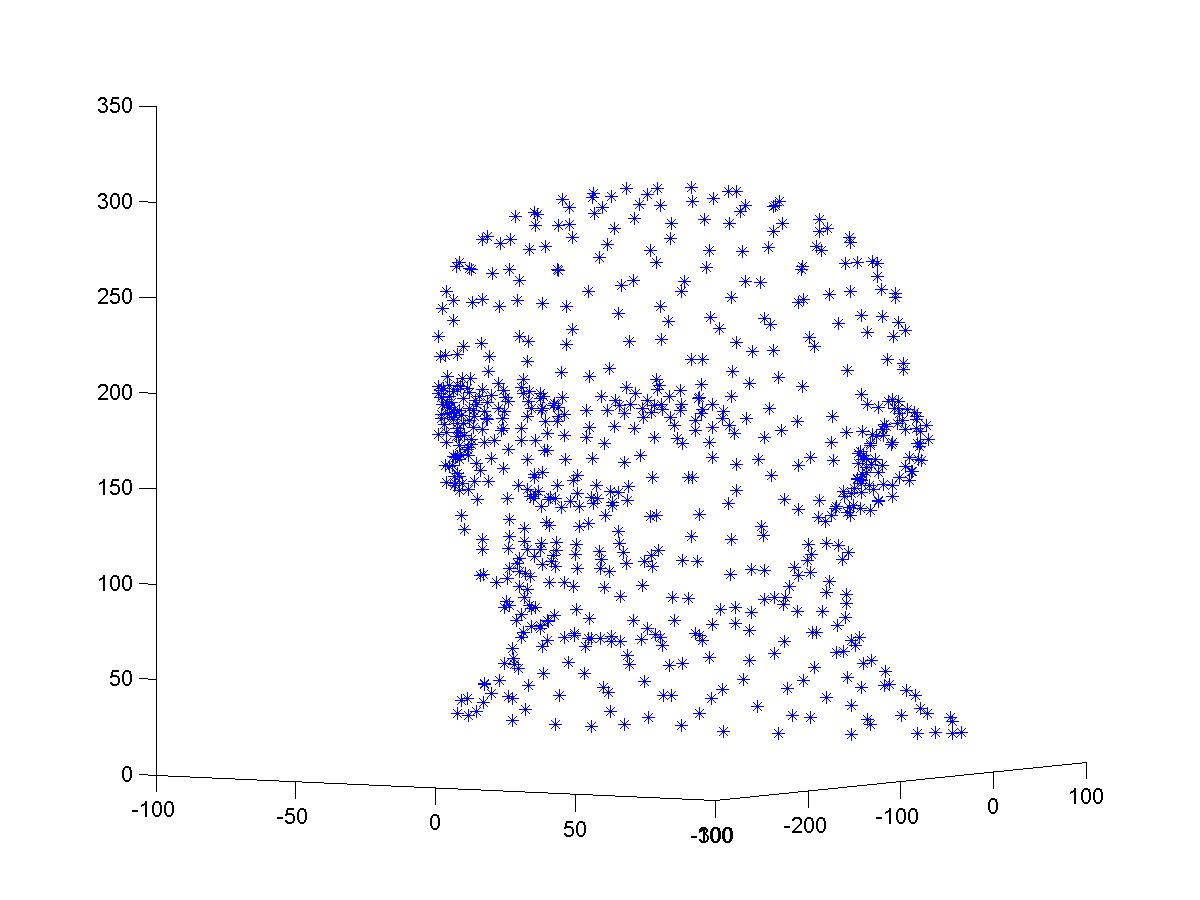
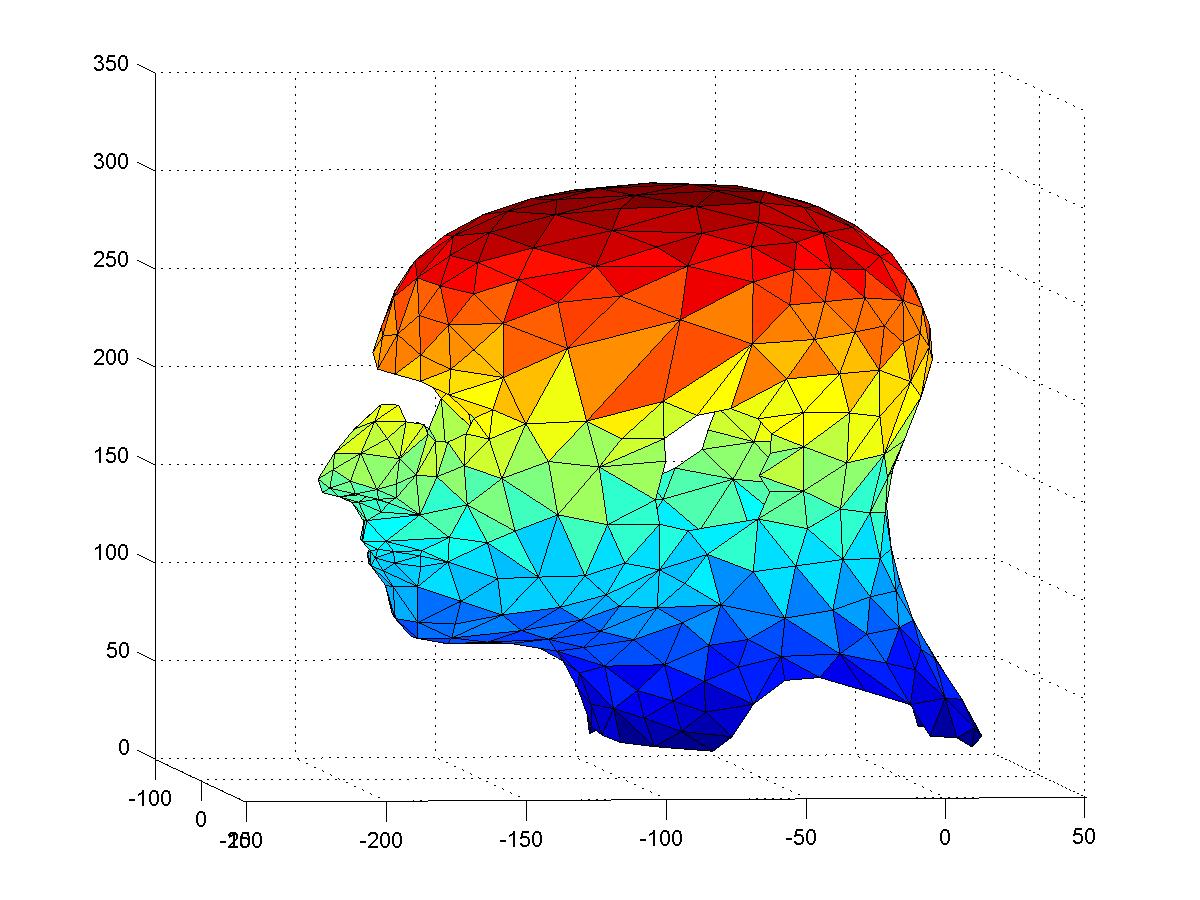
A set of point cloud is centeralizable if there exists a center O\in {\bf R}^3 such that for any point p in {\cal I}, the ray from O to p does not intercept any other point in the piecewise linear interpolant {\cal I}. When a point cloud is centeralizable, we can view the piecewise linar interpolant as a function defined on a spherical surface. The interpolant can be projected to the surface of the sphere to form a spherical triangulation of a polygonal domain of the spherical surface.
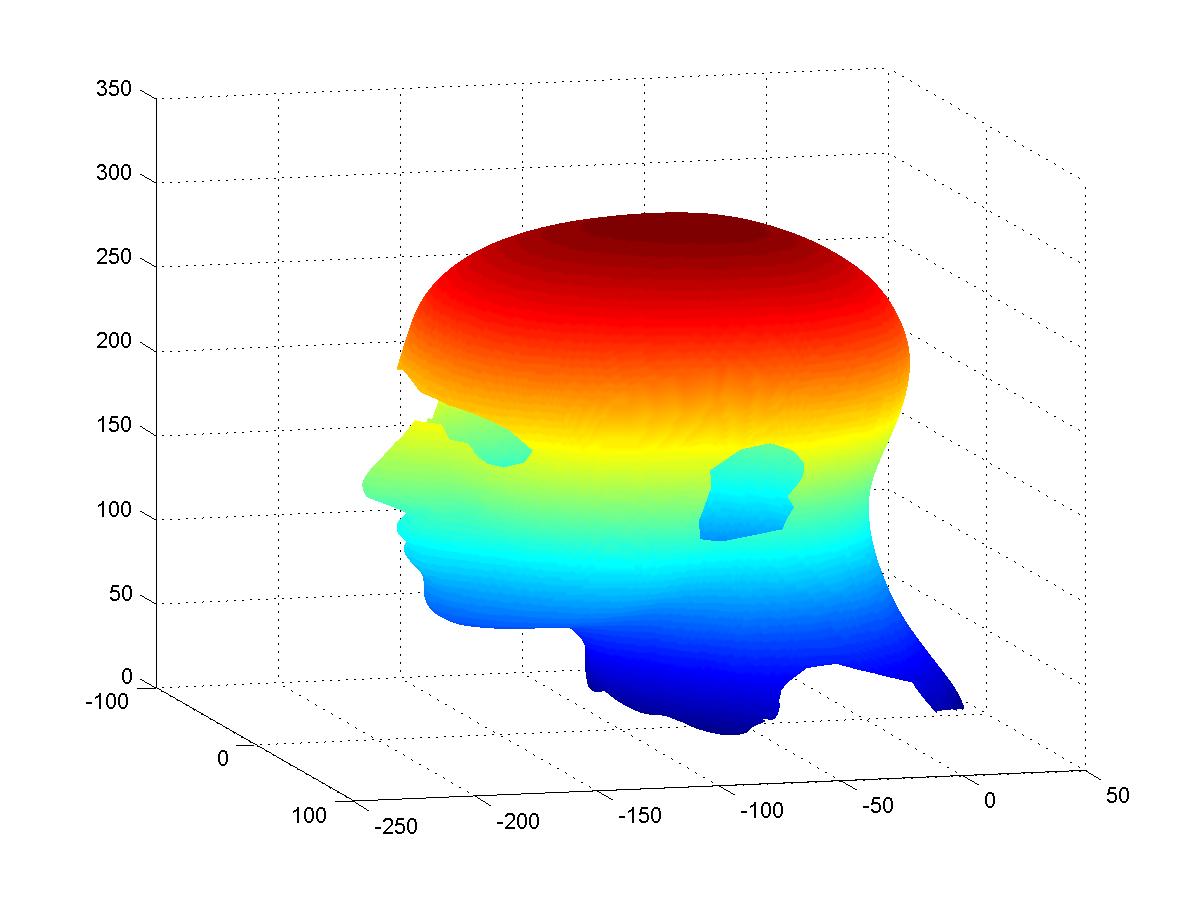
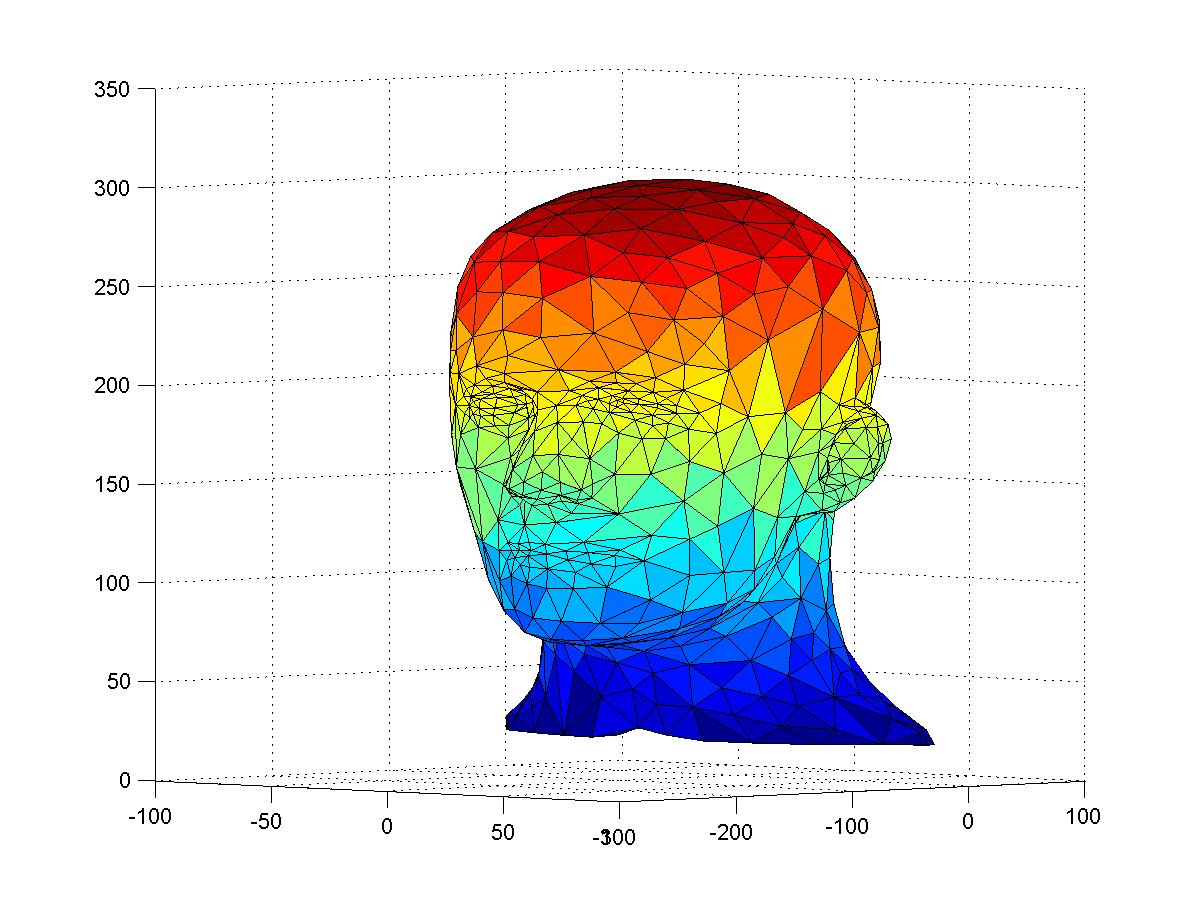
However the point cloud is not centeralizable near the areas of ears, eyes, and shoulders. After cutting off these areas, a modified point cloud is shown in the left of the following figures. A $C^1$ quintic interpolatory spherical spline surface can be found in based on modified point cloud using the algorithm described in the paper mentioned above. One of possible applications is to make customized wigs for cance patients.