Research
I have four research topics. One is Mjultivariate Splines and Their Applications, one is Sparse Solutons of Linear Systems and Their Applications, Graph Clustering by Sparse Solution Methods and Breaking the Curse of Dimensionality by using Kolmogorov Superposition Theorem. Let me explain them below:
Multivariate Splines
One of my main interests lies in the theory and application of multivariate splines which I have studied for over thirty years. The main reason that multivariate splines have interested me for so long is that it is a fundamental tool for approximating any unknown or known, but complicated functions conveniently.They can be very flexible in approximating functions in the sense that one can use splines of any degree, any smoothness over any triangulation/tetrahedral partitions or spherical triangulation. Typical applications are scattered data fitting
and interpolations over scattered locations, numerical solutions of partial
differential equations over domain of irregular shape, image enhancements, smooth curves and surface reconstruction,
function denoising, and data forecasting. Numerical Analysis, Scientific Computation, and Applied Mathematics in general need such a tool. I need to make the tool as convenient as possible and let as many people to know it as possible.
In theory, I mainly study the approximation properties of multivariate splines, construction of locally supported spline functions,
approximation properties of data fitting using multivariate splines, how to implement them efficiently, computational schemes using multivariate splines for applications. A typical paper that represents my work is On the Approximation Power of Bivariate Splines. They have various applications in data fitting, smooth surface reconstruction from given data and hole filling in Computer Aided Geometric Design, numerical solution of PDE, e.g. Fluid Flow Simulation, and in geodetic application, e.g. geopotential reconstruction. Bivariate Splines can be used for image enhancements as seen in these numerical results. I have used bivariate splines for statistical applications, e.g. to forecast ozone concentration level at Atlanta based on spatial data around Atlanta. We are able to predict the level
of ozone concentration very well. In particular, a usefulness of these multivariate splines can be seen in a Ph.D. dissertation at the aerospace engineering department of Delft University of Technology, Netherlands. Their usage for a global system of identification based on a NASA wind tunnel dataset and other data sets demonstrates their excellence, much better than other
data fitting methods. See Visser's Dissertation for detail. For another example, trivariate splines have been useful for study of extending battery life by finding optimal parameters from spline interpolation of experimental data values. The most recent usage of multivariate splines is to solve 2D/3D partial differential equations based on a multivariate spline collocation method. See Lai and Lee, 2022 in SIAM Journal of Numerical Analysis. We can achieve very accurate solutions of all second order elliptic PDEs.
"Spline Functions on Triangulations"  Larry Schumaker
and I wrote a monograph "Spline Functions on Triangulations" together which was published by Cambridge University Press in 2007.
Larry Schumaker
and I wrote a monograph "Spline Functions on Triangulations" together which was published by Cambridge University Press in 2007.
Wavelets I have used multivariate box splines to construct various wavelet functions and studied their application for image processing. My interest is to construct various compactly supported biorthogonal wavelets, tight wavelet frames, orthonormal wavelets in Sobolev spaces, and pre-wavelets in the multivariate setting using multivariate box splines. The regularity of these wavelets are inherited from the box spline functions used. Tight wavelet frames based on bivariate box splines are implemented and used for image edge detection and denoising. In addition, orthonormal wavelets, orthonormal multi-wavelets were constructed.
PDE/Numerical PDE I have used bivariate splines to numerically solve 2D Navier-Stokes equations, 2D Helmholtz equation with large wave number over bounded domains and exterior domain problems , 2D nonlinear biharmonic equations associated to a model for thin-films which are similar to Ginzburg-Laudau equations. I have used bivariate splines, finite element and finite difference
methods to solve time dependent and steady state nonlinear PDE associated with ROF model for image denoising.
 In addition to the use of wavelets for image processing, I am also interested in the PDE approach for image denoising, mainly using bivariate splines to solve the nonlinear PDE associated with ROF model for image denoising and use the
approach for image resizing, image imprinting, and image enhancements. Some numerical results can be found here
In addition to the use of wavelets for image processing, I am also interested in the PDE approach for image denoising, mainly using bivariate splines to solve the nonlinear PDE associated with ROF model for image denoising and use the
approach for image resizing, image imprinting, and image enhancements. Some numerical results can be found here
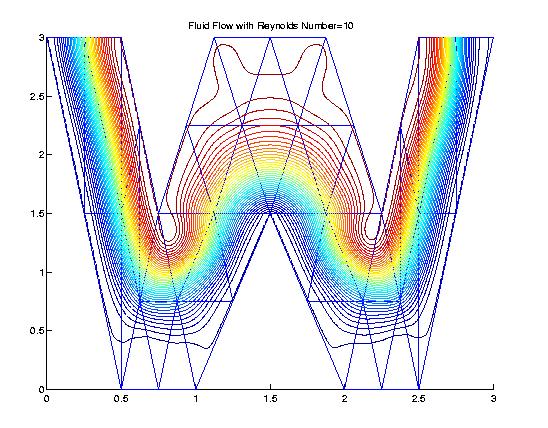
An application of multivariate splines for Fluid Flow Simulation won me a research medal from the University of Georgia in 2002.
The representative paper is Bivariate Splines for
Fluid Flows. In this paper, many standard fluid flows, e.g. cavity flows, backward step flows, flows around a circular object with various Reynolds numbers are simulated. In particular, a cavity flow over a triangular domain is
simulated. Flows passing through a narrowed channel is simulated. Bivariate
splines of various degrees were used in various simulations. The highest
degree I used is 12. In fact, the degree of splines is an input variable and
my matlab code is programmed for arbitrary degree $d\ge 1$, for arbitrary
smoothness $r\ge 0$ and arbitrary triangulation $\triangle$.
Multivariate Spline Approximation Currently, I am using bivariate splines to approximate the functions in ill-posed problems, e.g., de-convolution, to approximate functions of bounded variation (BV), to approximate probability density functions(PDF), and to approximate measurable functions (Learning Theory). More results are coming up soon.
Polygonal Splines The concept of spline functions over triangulation has been extended to spline functions over polygonal paritions. Michael Floater and I have used generalized barycentric coordinates(GBC) to construct continuous vertex splines over polygonal partition. See continuous polygonal splines of any degree and its numerical solution of the Poisson equation. A demo matlab code can be downloaded at the publication section of this webpage.
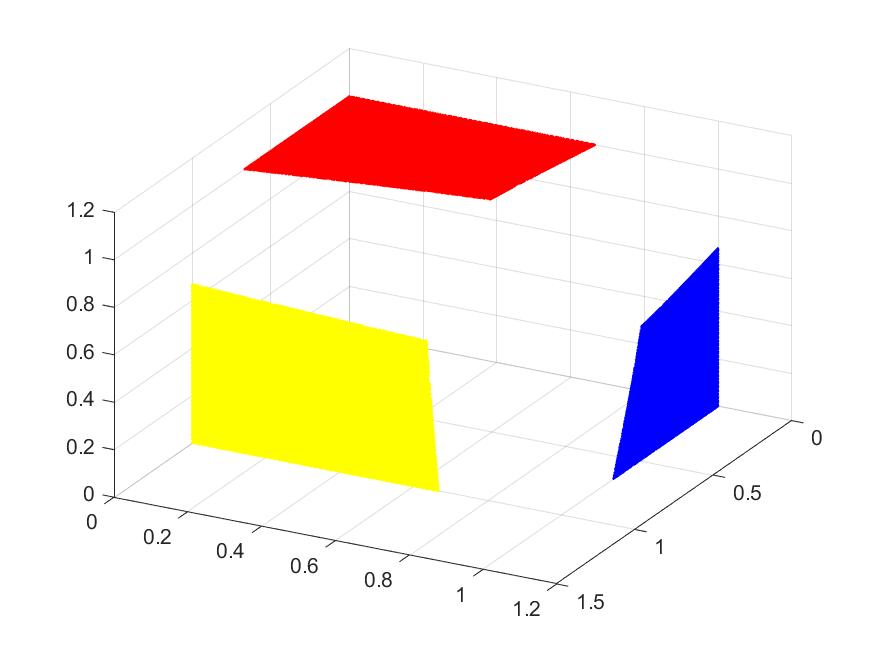
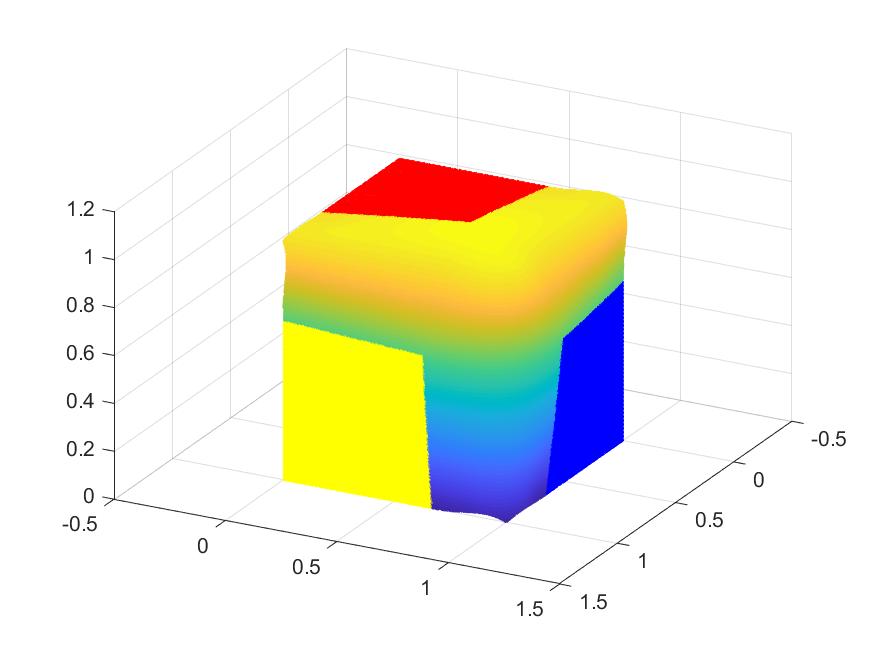 Smooth vertex splines are being constructed by James Lanterman, one of my former Ph.D.s. We are able to use them for surface constructions. See for surface construction, e.g. suitcase corners. That is, given three surfaces(in red, yellow and blue), we are able to construct a smooth connecting surface at the corner.
Smooth vertex splines are being constructed by James Lanterman, one of my former Ph.D.s. We are able to use them for surface constructions. See for surface construction, e.g. suitcase corners. That is, given three surfaces(in red, yellow and blue), we are able to construct a smooth connecting surface at the corner.
Compressive Sensing, Sparse Solution of Underdetermined Linear System, Low-rank Matrix/Tensor Completion, Phaseless Retrieval
I am also interested in sparest solutions of undetermined linear systems and their applications in compressed sensing, low-rank matrix recovery and graph clustering/community detection. In my joint paper with Simon Foucart, we show how to use quasi norm lq, 0 < q ≤ 1 to find the sparsest solution. This paper has many citations, more than 680 citations on Google Scholar
since its publication. I have worked with W. T. Yin on unconstrained lq minimization for sparse vector recovery and matrix completion recently.
Three joint papers have been published:
Improved Iteratively Reweighted Least Squares
for Unconstrained Smoothed lq Minimization and
Augmented l1 and Nuclear Norm Models with a Globally Linearly Convergent Algorithm.
In addition, I have several other preprints and reprints on this topic available on-line at my publication section of this page. I have worked with the group led by Dr. Jieping Ye on matrix completion and tensor completion. One joint paper has been published: Orthgonal Rank-One Matrix Pursuit for Low Rank Matrix Completion .
 It is believed that the algorithm in our paper is the most efficient algorithm for matrix completion. I have worked with Daniel Mckenzie to use compressive sensing techniques for finding graph clusters/communities. See our paper for detail. Our algorithm is also the most efficient one so far.
For example, we can use a sparse solution method to classify images.
It is believed that the algorithm in our paper is the most efficient algorithm for matrix completion. I have worked with Daniel Mckenzie to use compressive sensing techniques for finding graph clusters/communities. See our paper for detail. Our algorithm is also the most efficient one so far.
For example, we can use a sparse solution method to classify images.  See an example on the left.
For phase retrieval problem, with collaborators Meng Huang, Abraham Varghese, and Zhiqiang Xu, I have developed a DC (difference of convex functions) based method. Numerical performance is excellent in the sense that we can retrieve the exact solution of size n based on 2n measurements for real valued signals and 3n measurements for complex valued signals with large successful rate. For sparse solution of sparsity s which is less than n, we can retrieve it using 1.5n measurements with high probability. See for detail. Most recently, Yang Wang and I pulished a monograph on compressive sensing. The title is Sparse Solutions of Underdetermined Linear Systems and Their Applications.
Please check it out.
Recently, our sparse solution methods for graph clustering are experimented with a sucess for various image data. One of our papers was accepted for presentation in IJCAI 2023 with acceptance rate 14%.
See an example on the left.
For phase retrieval problem, with collaborators Meng Huang, Abraham Varghese, and Zhiqiang Xu, I have developed a DC (difference of convex functions) based method. Numerical performance is excellent in the sense that we can retrieve the exact solution of size n based on 2n measurements for real valued signals and 3n measurements for complex valued signals with large successful rate. For sparse solution of sparsity s which is less than n, we can retrieve it using 1.5n measurements with high probability. See for detail. Most recently, Yang Wang and I pulished a monograph on compressive sensing. The title is Sparse Solutions of Underdetermined Linear Systems and Their Applications.
Please check it out.
Recently, our sparse solution methods for graph clustering are experimented with a sucess for various image data. One of our papers was accepted for presentation in IJCAI 2023 with acceptance rate 14%.

 Twenty-two Ph.D. students have graduated under my supervision. They are in order of seniority, Dr. Wenjie He, Dr. Xiangming Xu, Dr. Gerard Awanou, Dr. V.Baramidze, Dr. K. Nam, Dr. J. Zhou, Dr. O. Cho, Dr. H. P. Liu, Dr. J. B. Wu, Dr. Bree Ettinger, Dr. Louis Y. Liu, Dr. Jane Hong, Dr. Leopold Matamba Messi, Dr. George Slavov, Dr. Abrahm Varghese, Dr. James Lanterman, Dr. Daniel Mckenzie, Dr. Clayton Mersmann, Dr. Yidong Xu, Dr. Kenneth Allen, Dr. Tsung-Wei Hu, and Dr. Jinsil Lee..
Twenty-two Ph.D. students have graduated under my supervision. They are in order of seniority, Dr. Wenjie He, Dr. Xiangming Xu, Dr. Gerard Awanou, Dr. V.Baramidze, Dr. K. Nam, Dr. J. Zhou, Dr. O. Cho, Dr. H. P. Liu, Dr. J. B. Wu, Dr. Bree Ettinger, Dr. Louis Y. Liu, Dr. Jane Hong, Dr. Leopold Matamba Messi, Dr. George Slavov, Dr. Abrahm Varghese, Dr. James Lanterman, Dr. Daniel Mckenzie, Dr. Clayton Mersmann, Dr. Yidong Xu, Dr. Kenneth Allen, Dr. Tsung-Wei Hu, and Dr. Jinsil Lee..  I received my Bachelor's
Degree from Hangzhou University which is now a part of Zhejiang University.
In 1984, I went to Texas A&M University for my graduate studies and began my life in United States of America. After obtaining my Ph.D. in 1989, I continued on to the University of Utah for three years of postdoctoral training.
Since 1992, I have been working at
I received my Bachelor's
Degree from Hangzhou University which is now a part of Zhejiang University.
In 1984, I went to Texas A&M University for my graduate studies and began my life in United States of America. After obtaining my Ph.D. in 1989, I continued on to the University of Utah for three years of postdoctoral training.
Since 1992, I have been working at